Three months have already passed since the beginning of the programme, and the only task that is still in my TODO list is the writing of this post as my Work Product Submission report. Let’s cross it out.

Disclaimer: This post will be quite technical and probably really boring if you are not very interested in the ROOT development.

Table of Contents

1. TL;DR
   1. What Have I Done?
   2. What Code Has Been Merged?
   3. What Code Has Not Been Merged?
   4. What Is Left To Do?
2. Detailed Final Report
   1. Previous State of ROOT
   2. Using The New Code
      1. Gradient and Fitting Interfaces
      2. Mathematical Functions
   3. Dissecting the Code
      1. Gradient and Fitting Interfaces
      2. Integrating Everything
      3. Nice Touches
   4. Result Analysis
3. Conclusions

TL;DR

If you just want to know what have been accomplished and the work that is left to do, you will find here a short description covering the highlights of my summer.

If you are brave enough and do not fear tricky details and documented decisions in the code design, go to the detailed section and enjoy.

What Have I Done?

In a few words, my work in ROOT can be summarised as the generalization of the fitting algorithms interfaces in order to have parallelized and vectorized implementations that make the algorithms, and thus the computations of the final user, more efficient.

What Code Has Been Merged?

At the end of the programme, three pull requests (PR) were merged:

• Gradient interfaces templated.

The most important work is done in this PR, where the gradient interfaces are generalized and the parallelized and vectorized versions of Chi2, LogLikelihood and PoissonLikelihood gradient evaluations are implemented. The whole PR was squashed into this one commit when it got merged into master.

• Fix execution policy error when IMT is OFF.

After the first PR was merged, we saw that some tests failed if IMT was disabled. The problem was that those tests tried to use the multithread execution policy in FitUtil even if no parallelization was enabled. This commit, that you can see here in the master branch, fixed this problem forcing the execution policy to be ROOT::Fit::ExecutionPolicy::kSerial while warning the user that such a change has been made.

• Add padding to all vectors in FitData and its children.

The classes storing the data in the fitting algorithms —FitData, BinData and UnBinData— play an important role in the vectorization. In order to ease the vectorization of the algorithms, this PR adds padding to every vector in these classes: the ones storing the coordinates, the data and the errors; assuring the length of the vectors is a multiple of the SIMD vector size. The commit merging this PR in the ROOT repo can be found here.

What Code Has Not Been Merged?

Three PRs remained unmerged at the end of the programme, but they contain useful work that should be used after GSoC finishes:

• Adaptation of fitting interfaces to templated gradient functions.

This PR completes the work of the fitting interfaces generalization, providing the user the possibility to use gradient functions in their fittings. It also adds integration tests to check everything works as a whole.

• Vectorization of TMath.

This second unmerged PR is part of an important ongoing work: the implementation of vectorized versions of the most important functions in TMath.

• Test evaluation of gradient of multidimensional functions.

This PR adds tests to check that the evaluations of the gradient of multidimensional functions, implemented in the first merged PR, are correct.

What Is Left To Do?

After GSoC finishes, the ROOT developers may want to complete some of the work I started during the summer that did not get merged before the final evaluation. In particular, the unmerged PRs should be finished and merged: the bug stopping the first PR to be merged should be fixed, the remaining functions in TMath should be vectorized and the failing test of the last PR should be inspected and the bug causing it should be fixed.

Detailed Final Report

Ok, so now that you have an overall idea of my summer work, I will describe the details and decisions behind the lines of code written through these months.

Previous State of ROOT

Before GSoC17, ROOT had a good set of interfaces for fitting data; see, for example, the section 5. Fitting Histograms of the User’s Guide to make an idea of what ROOT can do for you. However, these interfaces were tied to a specific base type; namely, they worked only with doubles. Furthermore, the code was first designed to serve as a set of serial algorithms, and parallelization was not taken into account.

Considerable work has been done before the programme in order to generalize these interfaces and add the possibility to use other types and other execution policies. See, for example, the struct Evaluate in FitUtil.h, where the evaluations of Chi2, LogLikelihood and PoissonLikelihood functions were adapted to have vectorized and parallelized versions.

However, a lot more work in this direction needed to be done, and my summer has mainly focused on providing the possibility to evaluate vectorized and parallelized vrsions of Chi2, LogLikelihood and PoissonLikelihood gradient functions.

Using The New Code

Ok, so we all know that my code has nice tricky details and the commits I did on the PRs are super cool, but before describing all the work that has been done, let’s see how to use the new methods and the good results we can obtain.

Gradient and Fitting Interfaces

To illustrate the main work done with the fitting interfaces and the gradients, we are going to inspect —a slightly simplified version of— the tests in testGradient.cxx.

These tests assume that the user have some data to fit into a model defined by the following function:

// Model function to test the gradient evaluation
template <class T>
static T modelFunction(const T *data, const double *params)
{
   return params[0] * exp(-(*data + (-130.)) * (*data + (-130.)) / 2) +
          params[1] * exp(-(params[2] * (*data * (0.01)) - params[3] * ((*data) * (0.01)) * ((*data) * (0.01))));
}

First of all, you would need to create a TF1 to hold your function with initial parameters and a TH1 to hold your data —here we have randomised data generated from the model function—. With the work done during the summer, you can now use data types other than double for your model functions, so let’s use here ROOT::Double_v:

// Create TF1 from model function and initialize the fit function
TF1 fModelFunction("TF1", modelFunction<ROOT::Double_v>, 100, 200, 4);

const Double_t fParams[4] = {1, 1000, 7.5, 1.5};
fModelFunction.SetParameters(fParams);

// Create TH1 and fill it with values from model function
unsigned fNumPoints = 12801;
TH1D fHistogram("TH1", "Test random numbers", fNumPoints, 100, 200);
gRandom->SetSeed(1);
fHistogram.FillRandom("TH1", 1000000);

Now we can use a wrapped TF1 object to store our fitting function and populate a BinData object with the data from the histogram.

ROOT::Math::WrappedMultiTF1Templ<ROOT::Double_v> fFitFunction(fModelFunction, 1);

ROOT::Fit::BinData fData;
ROOT::Fit::FillData(fData, &fHistogram, &fModelFunction);

And now to the fun part! We can create either a Chi2, PoissonLikelihood or LogLikelihood fitter with the vectorized fitting function and a multithread execution policy!

using GradFunc = ROOT::Math::IGradientFunctionMultiDimTempl<double>;
using BaseFunc = ROOT::Math::IParamMultiFunctionTempl<ROOT::Double_v>;

// You can instantiate a Chi2 fitter...
ROOT::Fit::Chi2FCN<GradFunc, BaseFunc> fFitter1(
   fData, fFitFunction,
   ROOT::Fit::ExecutionPolicy::kMultithread
);

// ... or a PoissonLikelihood fitter...
ROOT::Fit::PoissonLikelihoodFCN<GradFunc, BaseFunc> fFitter2(
   fData, fFitFunction, 0, true,
   ROOT::Fit::ExecutionPolicy::kMultithread
);

// ... or a LogLikelihood fitter.
ROOT::Fit::LogLikelihoodFCN<GradFunc, BaseFunc> fFitter3(
   fData, fFitFunction, 0, false,
   ROOT::Fit::ExecutionPolicy::kMultithread
);

Whatever the fitter you choose, what we can do now is to call its Gradient method:

Double_t solution[4];

// This is where the magic happens <3
fFitter1->Gradient(fParams, solution);

That this one last line works may seem trivial or unimportant, but it has been a lot of work and the results are really worth it! Check out the Result Analysis section to see a deeper study of the benchmarks done.

Mathematical Functions

In top of the generalization of the gradient interfaces, one important task has been started: the vectorization of the functions in TMath. This will be also completely transparent to the final user.

For example, look at the differences between using the scalar and vectorized versions of TMath::Gaus. Assuming that we are on a machine where the size of a ROOT::Double_v vector is 2 and that vectorizedData is a ROOT::Double_v that contains the same values that data1 and data2, both of type double; the output from this:

// Scalar version
std::cout << TMath::Gaus(data1) << ", " << TMath::Gaus(data2) << std::endl;

will be the same as the output from this:

// Vectorized version
std::cout << TMath::Gaus(vectorizedData) << std::endl

Yes, that’s true. The only difference is the type of the value passed to the functions and the output returned from them. The latter version would be, of course, approximately two times faster than the first. How cool is that?

Dissecting the Code

Now that we know how to use the new code and how the final user will see the efficiency of its code automatically improving, we will explain in this section the technical details of the work done through the summer, studying the most important commits of the PRs done. Let’s go!

Gradient and Fitting Interfaces

Let us now describe in detail the main work of this project, implemented in this PR. Let us inspect every commit to see what I did and why:

• Commit 16cbcb5 : The very first commit I pushed to my ROOT fork implemented a parallelized version of the method FitUtil::EvaluateChi2Gradient. This was pretty direct, as I just had to add a new version of the method using the parallelization techniques provided by ROOT; in particular, ROOT::TThreadExecutor::MapReduce. This was implemented following the example of the method FitUtil::EvaluateChi2, which was already parallelized in the Evaluate struct. The finished implementation can be seen in the file FitUtil.cxx, method FitUtil::EvaluateChi2Gradient.
• Commit b705cf4 : This commit implemented a really important work, as all the remaining commits depended greatly on it: the generalization of the gradient interfaces; namely:
  • In IFunction.h, the interface IGradient{,Function}MultiDim was templated, keeping its double specialization in IFunctionFwd.h as a typedef that matched the old name in order to preserve backwards compatibility.
  • In ParamFunction.h, the interface IParametricGradFunctionMultiDimTempl was adapted to use the new IGradientFunctionMultiDimTempl, and the gradient-related methods were templated as well.
• Commit f48ee1d: While the previous commit templated the gradient interfaces, this one templated the gradient implementations; namely:
  • The method TF1::GradientPar, in TF1.h, was templated and its vectorized version was implemented.
  • The methods WrappedMultiTF1Templ::ParameterGradient and DoParameterDerivative in WrappedMultiTF1.h were templated. In this case, I needed to use some tricks to bypass cases where TFormula::EvalPar was called, as it is not vectorized yet.
• Commit cad190c: After the previous commit had made the vectorization scenario possible, this one tested it out by implementing a vectorized (and parallelized) version of FitUtil::EvaluateChi2Gradient.
• Commit 448b894: To test the previous work, a GoogleTest was added. The previous study on the test is based on the work done here.
• Commits d81308c, 7da041d, 66a4d9b, 3acfc87 and 2ef06c9 introduced a bunch of refactors and bug fixes, but they are not that important to understand the whole of the work done.
• Commit bd8a250: This commit introduced an important change, as it modified a critical method, TF1::GradientPar, to make it thread-safe. It was necessary that this method was thread-safe, otherwise, the parallelizations that would use it would have been unsafe. Before this commit, TF1::GradientPar modified the private member fParameters. In a multi-threaded scenario, this produced race conditions when other threads needed to access this same member. Now, GradientPar modifies a local copy of fParameters. Others techniques to make the method thread-safe were studied, but all of them were rejected:
  • Making fParameters thread_local: this first option did not make sense, as fParameters is a non-static member and thus cannot be made thread_local.
  • Using a mutex to atomically call GradientPar: to decide between this option and the one that was finally implemented, I did a quick benchmark, and saw that implementing the mutex made the parallelized version even slower than the original one, but always copying the vector inside GradientPar made the original version slower than before (although the parallelized version was in that case faster, as expected).
• Commit 33229b3: This is a huge commit that implemented both parallelized and vectorized versions of the gradients of the two remaining fitting methods: PoissonLikelihood and LogLikelihood. I also added here tests to check that these new implementations were correct. This commit, then, can be thought as the union of the first, fourth and fifth described commits, but instead of focused on Chi2, it was focused on both PoissonLikelihood and LogLikelihood.
• Commit 66db096: Final commit to adapt to a change to the codebase that was made while I was working in my local branch.

Integrating Everything

After the generalization of the gradient interfaces and the implementation of the gradient evaluation of the three main functions in the fitting algorithms, we still have one thing to do: to integrate everything so that the user do not have to worry about the details behind the calls they make. And here it comes one of the unmerged PRs, where ROOT::Fit::Fitter is adapted so that it can work with functions with templated gradients. This way, the user will be able to call the Fit method, so that they have nothing to change in their code but it is still way more efficient.

Let’s see the two unmerged commits to know how the integration is made:

• Commit df7bb2d: The main work of this PR is done here. In top of the IGradModelFunction used by the Fitter class, this commit adds a new typedef for the vectorized model functions with gradient: IGradModelFunction_v. The main changes can be found on Fitter::DoLeastSquareFit, Fitter::DoBinnedLikelihoodFit and Fitter::DoUnbinnedLikelihoodFit, that perform the fit using the now well-known classes Chi2FCN, PoissonLikelihoodFCN and LogLikelihoodFCN, respectively. Here, the commit adds one case uncovered until now: the case for vectorized functions with implementing the gradient interface. The new code handles the case calling the *FCN classes correspondingly, using the work done until now in the main PR.
• Commit 59e3fb9: To check that the new code works, the scalar, vectorial, unbinned and binned fitting cases are tested here. These tests are the reason why the PR is still unmerged, as they expose one bug that make the unbinned fit test fail.

Here we should also talk about one of the other merged PRs: the one adding the padding to all vectors in FitData and its children. FitData is basically a wrapper of an std::vector, and to ease the vectorization and the vectorized loops on the fitting data, this PR pushes a single commit that generalizes the notion of padding to all coordinates, data and error vectors that are abstracted out by FitData, BinData and UnBinData. The idea behind this is to assure that the length of these vectors is always a multiple of the SIMD vector size, so that when we loop over them jumping as many elements as one vector can hold, we do not get into the terrifying world of uninitialised memory. This PR just adds a static function, FitData::VectorPadding, that computes the remaining of elements that should be artifiacilly added to a vector in order to have a length that is a multiple of the SIMD vector size. This function is then used throughout the initialising and resizing code of FitData and its children to ensure that everything is safe for the final user.

Nice Touches

Just to finish this report, we should talk about the ongoing work of vectorizing the functions in TMath. This work is started by this unmerged PR. Here, I added vectorized implementations of six functions:

• TMath::Min
• TMath::Gaus
• TMath::BreitWigner
• TMath::CauchyDist
• TMath::LaplaceDist
• TMath::LaplaceDistI

These versions, implemented in TMathVectorized.cxx, are good examples to know how to vectorize any function in TMath.

I have followed the same procedure with all previous functions in order to implement their vectorized versions so, as an example, we can study TMath:Gaus comparing the old serial code with the new vectorized version.

The code for the serial case can be see here:

Double_t TMath::Gaus(Double_t x, Double_t mean, Double_t sigma, Bool_t norm)
{
   if (sigma == 0) return 1.e30;
   Double_t arg = (x-mean)/sigma;
   // for |arg| > 39  result is zero in double precision
   if (arg < -39.0 || arg > 39.0) return 0.0;
   Double_t res = TMath::Exp(-0.5*arg*arg);
   if (!norm) return res;
   return res/(2.50662827463100024*sigma);
}

The code for the vectorized case is the following:

template <class NotCompileIfScalarBackend =
          std::enable_if<!(std::is_same<double, ROOT::Double_v>::value)>>
ROOT::Double_v Gaus(ROOT::Double_v &x, Double_t mean = 0, Double_t sigma = 1,
                    Bool_t norm = kFALSE)
{
   if (sigma == 0)
      return vecCore::NumericLimits<ROOT::Double_v>::Infinity();

   ROOT::Double_v arg = (x - mean) / sigma;

   // Compute the function only when the arg meets the criteria
   ROOT::Double_v res = vecCore::Blend<ROOT::Double_v>(
      vecCore::math::Abs(arg) < 39.0,
      vecCore::math::Exp(-0.5 * arg * arg),
      0.0);

   return norm ? res / (2.50662827463100024 * sigma) : res;
}

The first thing that we can see is that there is a SFINAE technique to compile the vectorized version only if the type ROOT::Double_v is different from double. This is required because there are some configurations in the building of ROOT that can make ROOT::Double_v to be just a typedef of double; if that occurs, we don’t want to compile a version re-implementing the same function, so that first template line make the compiler ignore the definition in that case.

The body of the two functions is basically the same, with the exception of the types and the branching code. When you are writing vectorized code with VecCore, you must take care of all the if statements you find. VecCore uses vectorization masks to implement the logic of branching, as we are dealing with several values that can react differently to a same condition.

For example, you can see that the code branches depending on the absolute value of arg. This branching is implemented in the vectorized version using the Blend function from VecCore library, that takes a mask as a first argument, the value that should be returned in case the condition is met as the second argument, and the value to return if the condition is not met as the third and last argument. This way, we can assign the correct value to every element in a vector.

There are some subtleties in the vectorization of functions, but for implementing a vectorized version of any TMath function Foo you just have to follow these steps:

1. Copy the Foo header from TMath.h and paste it in TMathVectorized.h.
2. Add the template <class NotCompileIfScalarBackend> line to make sure the vectorized version is compiled only when needed.
3. Modify the type of the input data to its vectorized version —double should be converted to ROOT::Double_v, int should be converted to Int_v…—, taking care that the functions cannot use a vectorized type passed by value: use references everywhere!
4. Modify the return type if needed.
5. Translate the body from the scalar case making sure the branching is implemented correctly using the vectorized masks.
6. Implement a test in math/mathcore/test/vectorization directory checking that the vectorized version behaves exactly like the scalar one. You can take a look at the examples there and copy its structure!

These are the steps I have followed to implement those functions, and they could serve as a way to implement new vectorized versions of the remaining functions in TMath.

Result Analysis

In order to analyse the efficiency of the work done during the summer, some benchmarks have been implemented. We are gonna study here the test implemented in testGradient.cxx, that works also as a benchmark, measuring the speedups of the new implementations.

First of all, the specs of the machine where the implementations were benchmarked:

• Vectorial intruction set: SSE4.2
• Number of cores: 4

With this machine, I have benchmarked 9 different situations, all of them defined in testGradient.cxx by using the following three different scenarios for the three gradient evaluations modified —Chi2, LogLikelihood and PoissonLikelihood—:

• Scalar and multithread evaluation; i.e., the evaluation of the gradient is parallelized only in the data level by using several threads.
• Vectorial and serial evaluation; i.e., the evaluation of the gradient is parallelized in the instruction level by using vectorization techniques.
• Vectorial and multithread evaluation; i.e., the evaluation of the gradient is parallelized both in the data and instruction level by using several threads along with vectorization techniques.

Before discussing the numbers obtained, let’s see the ideal cases; i.e., how good can the new implementations be.

As the benchmarking machine implementes the SSE4.2 instruction set, the number of elements in a ROOT::Double_v, i.e., a vector of double, is 2. Then, a vectorized implementation of any code can be, at most, 2 times faster than a scalar implementation.

On the other hand, as the number of cores is 4, a multithread implementation can be, at most, 4 times faster than a serial implementation.

Combining these two cases, we know we can get evaluations 8 times faster than the scalar serial case in an ideal scenario where the vectorization and multithreading do not add any overhead.

The tests measure the time spent in the call of the Gradient method of Chi2FCN, LogLikelihoodFCN and PoissonLikelihoodFCN. This measure is repeated 1000 times in order to compute the mean time. Then, we can compute the speedup of the benchmarked cases with respect to the scalar serial case. The results of the benchmark in the described machine are summarised in the following graph:

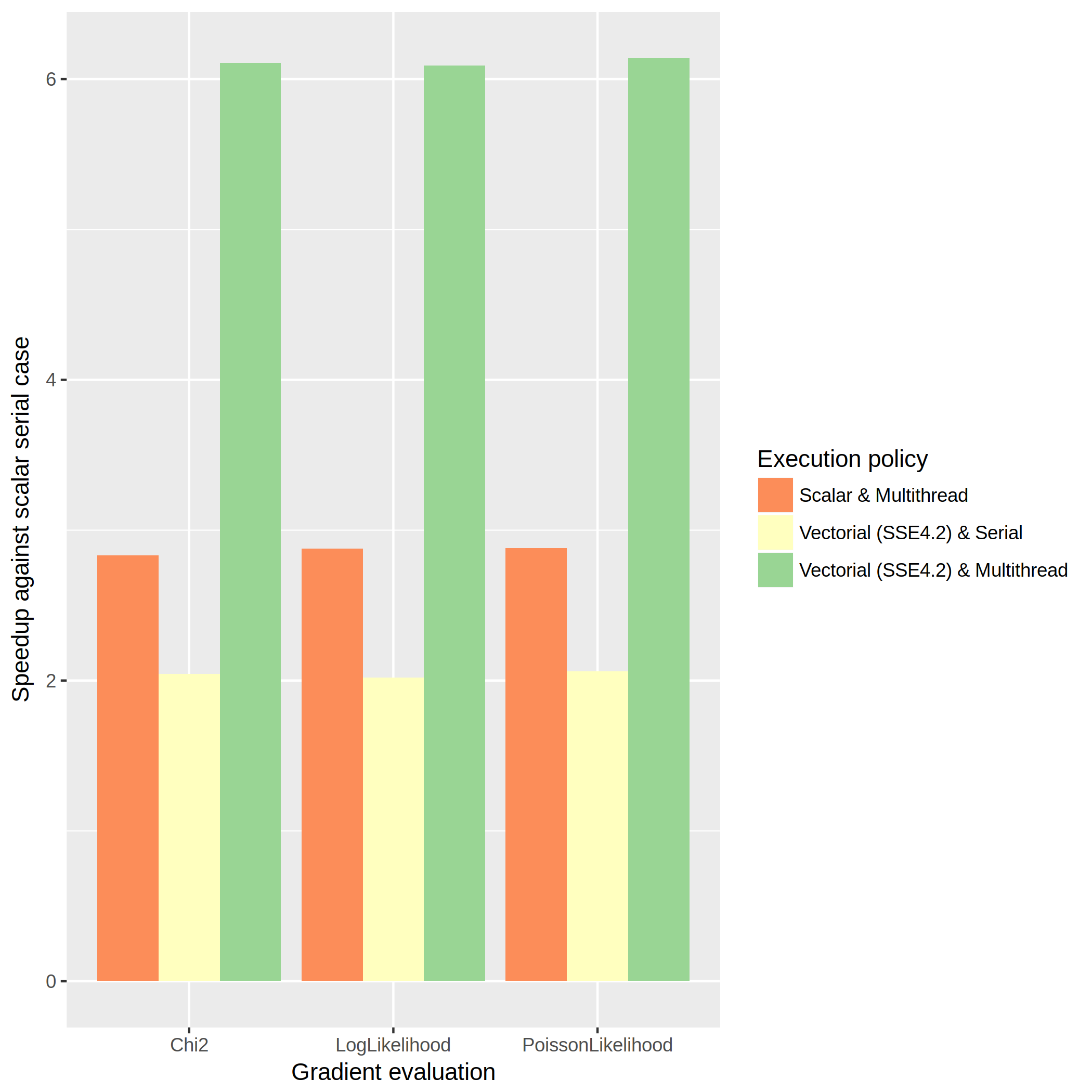
As you can see, the orange bars show the speedup when using the multithread implementations. The yellow ones show the speedup of the vectorized implementations. Finally, the green bars show the speedups of the implementations that use both the multithread and vectorized techniques.

First of all, we can see that the vectorized implementation is nearly ideal, as all the speedups in the yellow bars are near 2. This can be explained because there is no branching in the vectorized implementations of the Gradient method and the overhead of the calls to the vectorial instructions is zero compared to the call to the scalar ones. Then, the ideal case is reached and a speedup of ~2 is obtained.

The multithread scenario is however not that close to the ideal case: the speedups obtained with the multithread policy —orange bars— are nearly 3, out of the ideal speedup of 4 we could obtain. This in turn lower the expectations for the vectorized and multithread case, where we obtain speedups slightly greater than 6 —green bars—, out of the ideal case of an 8x improvement.

As an initial analysis, it is clear that the calls to ROOT::TThreadExecutor methods add some overhead to the implementations, so the ideal case cannot be reached. This is expected; however, further analysis of the multithread case should be done, which would of course improve also the combined scenario.

For example, a future benchmark should measure how the number of chunks in which the data is separated affects the speedups, analyse the exact overhead of the ROOT::TThreadExecutor methods and study the map function implemented in the evaluations.

In conclusion, although there is still room for some improvement, the benchmark is in general very good, and the speedups obtained will be really useful to the final users.

Conclusions

This summer has been as fun as hard, I learned way more than I expected at the beginning —and I expected to learn a lot— and I am really happy to have contributed to this big complex interesting project. Furthermore, it has been awesome to work in it with my mentors Xavier and Lorenzo, to whom I have to thank all their help throughout these three months.

I have learned all kind of subtleties of C++, I have understood that I knew nothing about git until now, I have learned about processors, vectorization techniques and low-level issues I did not know they even existed, I have improved my communication skills with other developers, I have really grasped the idea of open source contribution in a big project… In conclusion, I have enjoyed the programme in so many levels that I am sure it will be one of the most useful experiences I will have —at least in the near future—.

I hope my work is useful for the ROOT users and that my code is clear enough for the developers that will have to read it in the future!